Block Theory
This is a brief introduction to Block Theory (also known as "Key Block Theory"). To find more detailed information about Block Theory, please read the references listed at the end of this page.
Background
Currently, the projects involves the construction of rock (slope, foundation, underground caverns) have become increasingly frequent. Rock engineering analysis, i.e. through various means and ways to get a correct understanding of the laws of rock deformation and failure, to determine the stability conditions of rock mass, predict future changes, and devise effective measures to deal with the project, becomes more and more important. Block Theory is one of the most famous traditional analysis methods for these purposes in computational rock mechanics.
Brief History
- Beginning: Stereographic Method for Stability Analysis of Discontinuous Rocks in Scientia Sinica (Series A) 1977, by Gen-hua Shi
- Grow up: A Geometric Method for Stability Analysis of Discontinuous Rocks in Scientia Sinica (Series A) 1982, by Gen-hua Shi
- Establishment: Application of Block Theory to Simulated Joint Trace Maps in Proceedings of International Symposium on Fundamentals of Rock Joints, 1985, by Gen-hua Shi, Richard E. Goodman and J. P. Tinucci
- Mature: Richard E. Goodman and Gen-hua Shi, Block Theory and its Application to Rock Engineering, published in 1985
Main Concepts
Analysis Subject
The rock blocks created by intersections of discontinuities, including:
- joint surfaces (planes): Geological interfaces formed with a certain direction, size, shape and characteristics in the rock body
- free surfaces (planes): Contact faces between the rock and the outside air (e.g. the excavation surfaces)
Basic Assumptions
- All the surfaces are assumed to be perfectly planar (describe block morphology by linear vector equations)
- Joint surfaces are assumed to extend entirely through the volume of interest (infinite plane)
- Blocks defined by the system of joint faces are assumed to be rigid
- The discontinuities and the excavation surfaces (joint and free planes) are assumed to be determined as input parameters (the influence of variations in the joint set orientations will not be pursued in Block Theory)
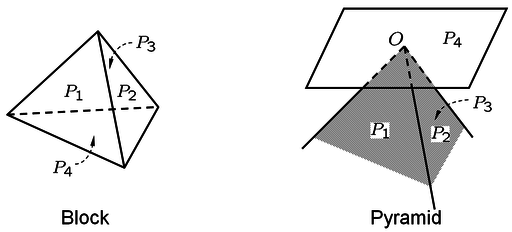
Block and Pyramid
- Block: space region surrounded by the actual planes (the intersection of half spaces), represent the shape and size of the actual rock block
- Pyramid: the intersection of half-spaces defined by the planes moved to the origin
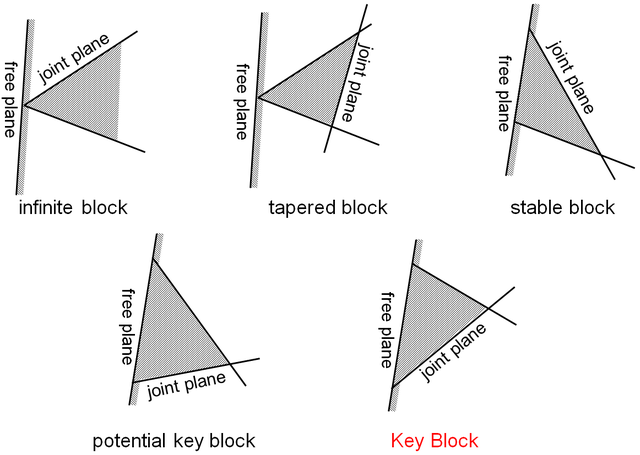
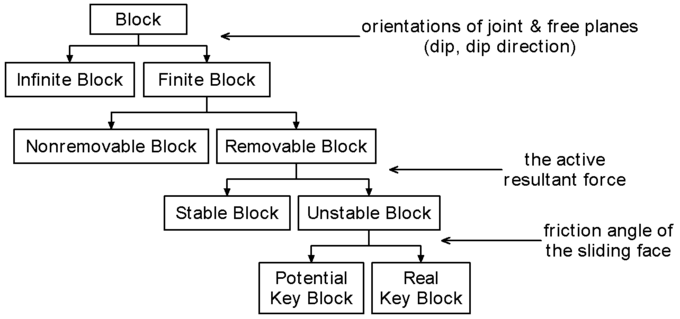
Block Classification
- Infinite Block: connected to the base rock mass, provides no hazard to an excavation as long as it is incapable of internal cracking
- Finite Block: cut by the joint and free planes, are divisible into removable and nonremovable types
- Nonremovable Block: has tapered shape and cannot be removed from the rock mass
- Removable Block: nontapered, finite block
- Stable Block: stable even without friction with respect to the resultant force
- Potential Key Block: stable with sufficient friction, potentially unstable
- Key Block: not only removable but oriented in an unsafe manner so that it is likely to move unless restraint is provided
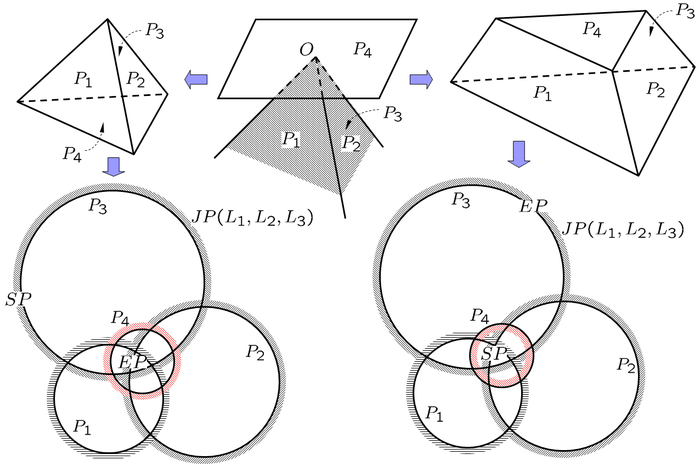
Examples (2D):
Pyramid Types
- (Joint Pyramid): the intersection of half-spaces defined by the joint planes moved to the origin
- (Excavation Pyramid): the set of shifted excavation half-spaces
- (Space Pyramid): the set of directions that is complementary to , i.e.
- (Block Pyramid): the intersection of the joint pyramid and the excavation pyramid, i.e.
Analysis Method
Problem Description
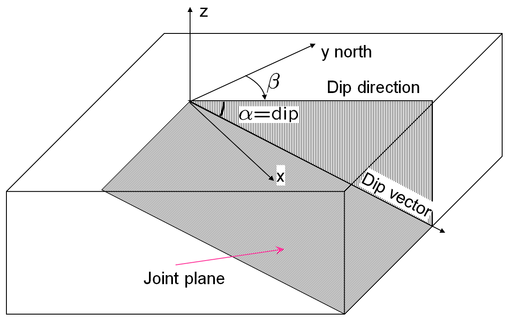
- Input: the parameters of joint and free planes (dip, dip direction, friction angle, etc.)
- Output the description of key blocks (shape, size, movement mode, etc.)
Mathematical Descriptions
- Plane:
- Half-space:
- Block:
Plane Equations Setup
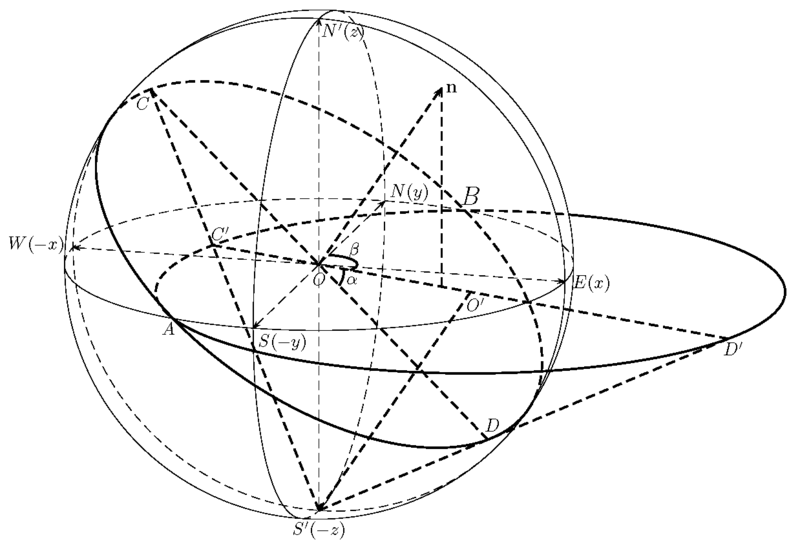
Stereographic Projection
The projection of the big circle on the sphere (intersected by the plane and the sphere through the origin) onto the equatorial plane is also a circle. Its center is:
Its radius is:
Analysis Steps
- Determine the plane equations of joint surfaces
- Calculate stereographic projection
- Set up all joint pyramids
- Analyze the stability and movement mode for each joint pyramid
- Find the key blocks from the joint pyramids combined with free planes
Theorem of Finiteness and Removability
The judgement for finiteness and removability (the preconditions for key block) of convex blocks can be done by following two theorems in classical block theory:
- Theorem of Finiteness
- A convex block is finite if its block pyramid is empty. Conversely, a convex block is infinite if its block pyramid is not empty.
- Theorem of Removability
- A convex block is removable if its block pyramid is empty and its joint pyramid is not empty. A convex block is not removable (tapered) if its block pyramid is empty and its joint pyramid is also empty.
Removability and Stereographic Projection
Modes of Sliding
Sliding Directions
The angle between the sliding direction () and the resultant force direction () is minimum from all the possible sliding directions:
- Lifting (free translation, falling): the sliding direction is the same as the resultant force, i.e. is contained inside but not in its boundary
- Single-face Sliding: the sliding direction lies within only one plane
- Double-face Sliding: the sliding direction is simultaneously in two planes
Sliding Force
A fictitious force $f\norm{s}$ for making a condition of limiting equilibrium:
- Lifting:
- Single-face Sliding:
- Double-face Sliding:
where
Judgement
- : the block tends to slide unless artificial support is added
- : the block is safe from sliding
Softwares
- easyKBT: A software with GUI for Key Block Theory, developed by Engineering Computing Center, UCAS.
- VisKBT: A software for 3D visualization of Key Block Theory, developed by Engineering Computing Center, UCAS.
References
- Gen-hua Shi. Stereographic Method for Stability Analysis of Discontinuous Rocks. Scientia Sinica (Series A), Vol.3, pp.260-271, 1977.
- Gen-hua Shi. A Geometric Method for Stability Analysis of Discontinuous Rocks. Scientia Sinica (Series A), Vol.15, pp.318-336, 1982.
- Gen-hua Shi, Richard E. Goodman and J. P. Tinucci.Application of Block Theory to Simulated Joint Trace Maps. in Proceedings of International Symposium on Fundamentals of Rock Joints, pp.367-383, 1985
- Richard E. Goodman and Gen-hua Shi. Block Theory and its Application to Rock Engineering, New Jersey: Prentice-Hall Inc., 1985.
- Gen-hua Shi and Richard E. Goodman. The Key Blocks of Unrolled Joint Traces in Developed Maps of Tunnel Walls. International Journal for Numerical Analytical Methods in Geomechanics, Vol.13(2), pp.131-158, 1989.
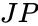 (Joint Pyramid): the intersection of half-spaces defined by the joint planes moved to the origin
(Joint Pyramid): the intersection of half-spaces defined by the joint planes moved to the origin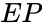 (Excavation Pyramid): the set of shifted excavation half-spaces
(Excavation Pyramid): the set of shifted excavation half-spaces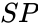 (Space Pyramid): the set of directions that is complementary to
(Space Pyramid): the set of directions that is complementary to 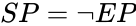
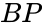 (Block Pyramid): the intersection of the joint pyramid and the excavation pyramid, i.e.
(Block Pyramid): the intersection of the joint pyramid and the excavation pyramid, i.e. 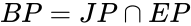
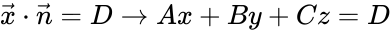
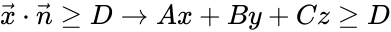
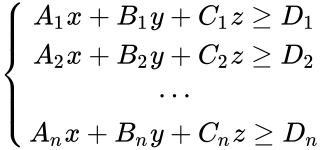
![{\displaystyle {\begin{aligned}A_{i}x&+B_{i}y+C_{i}z=0\\A_{i}&=\sin(\alpha _{i})\sin(\beta _{i})\\B_{i}&=\sin(\alpha _{i})\cos(\beta _{i})\\C_{i}&=\cos(\alpha _{i})\\{\hat {\mathbf {n} }}_{i}&=[A_{i},B_{i},C_{i},0]^{\mathsf {T}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/f63aef7058ec952d9cf7d0e0f1471ab3153db83a)
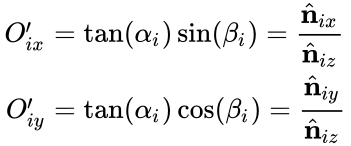
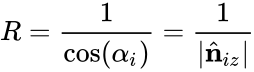
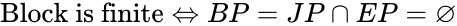
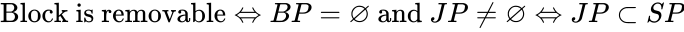
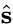 ) and the resultant force direction (
) and the resultant force direction (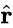 ) is minimum from all the possible sliding directions:
) is minimum from all the possible sliding directions:
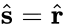
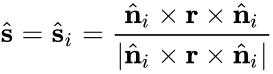

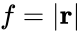
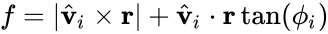
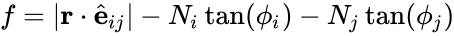

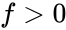 : the block tends to slide unless artificial support is added
: the block tends to slide unless artificial support is added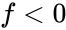 : the block is safe from sliding
: the block is safe from sliding